FirstOrder Linear Differential Equations from Chapter 16 / Lesson 3 19K In this lesson you'll learn how to solve a firstorder linear differential equation We first define what such an y(x)=2/(x^2C) Let's separate our variables, IE, have each side of the equation only in terms of one variable This entails dy/y^2=xdx Integrate each side intdy/y^2=intxdx 1/y=1/2x^2C Note that we would technically have constants of integration on both sides, but we moved them all over to the right and absorbed them into C Now, let's get an explicit solution I'm at the beggining of a differential equations course, and I'm stuck solving this equation $$(x^2y^2)dx2xy\ dy=0$$ I'm asked to solve it using 2 different methods I proved I can find integrating factors of type $\mu_1(x)$ and $\mu_2(y/x)$If I'm not wrong, these two integrating factors are $$\mu_1(x)=x^{2} \ \ , \ \ \mu_2(y/x)=\left(1\frac{y^2}{x^2}\right)^{2}$$
Secure Media Collegeboard Org Digitalservices Pdf Ap Ap16 Calculus Ab Q4 Pdf
Solve (1+x^2)dy/dx+y=e^tan^-1x
Solve (1+x^2)dy/dx+y=e^tan^-1x-Separable Variables (22) 1 Separable Equations A first order differential equation is said to be separable if it is of the form dy dx!Calculus Find dy/dx y^2= (x1)/ (x1) y2 = x − 1 x 1 y 2 = x 1 x 1 Differentiate both sides of the equation d dx (y2) = d dx ( x−1 x1) d d x ( y 2) = d d x ( x 1 x 1) Differentiate the left side of the equation Tap for more steps




Engineering Mathematics Notes
The equation is separable so you separate the variables and integrate both members of the equation (dy)/(dx) = frac (x2) x dy= frac (x2) x dx int dy= int frac (x2) x dx y = int dx 2 int (dx)/x y = x 2 ln x CSolve the Differential Equation dy/dx=xy^2 In this tutorial we shall evaluate the simple differential equation of the form d y d x = x y 2 by using the method of separating the variables The differential equation of the form is given as d y d x = x y 2 Separating the variables, the given differential equation can be written asClick here👆to get an answer to your question ️ Solve dy/dx = x^2 xy/x^2 y^2
The equation y = xc tells you nothing because c can take any value It is literally as useful as saying 0 = 0 It doesn't make any sense to manipulate dy/dx = y/x in the first place if you understand what that equation actually means, and this tutorial does not explain that to the readerExample Solve dy/dx = y(3 x);G!x"h!y" 2 Method of Separation of Variables Observe that a separable equation can be written as 1
Dy = −ey sin2xdx, e2y −1 ey dy = − sin2x cosx dx, usamos la identidad trigonométrica sin2x =2sinxcosx, µ ey − 1 ey ¶ dy = − 2sinxcosx cosx dx, ¡ ey −e−y ¢ dy = −2sinxdx, Z ¡ ey −e−y ¢ dy =2 Z (−sinx) dx Solución implícita ey e−y =2cosxc 1 Si usamos el coseno hiperbólico coshy = e ye− 2, podemos obtener Solve x^2 ( dy(x))/( dx) y(x) = 2 e^(1/x) x^3 Rewrite the equation 2 e^(1/x) x^3 y(x) x^2 ( dy(x))/( dx) = 0 Let R(x, y) = 2 e^(1/x) x^3 y and S(x, yAnswer to Solve the initial value problem dy/dx = (y^2 1)/(x^2 1), y(2) = 2 By signing up, you'll get thousands of stepbystep solutions to




Consider The Differential Equation Y 2 Dx X 1 Y Dy 0 If Y



How To Find Dy Dx Of E X E Y E X Y Quora
Math Differential equations VS A Spherical balloon is being inflated at the rate of 35cc/min The rate of increase in the surface area (in cm2/min) of the balloon when its diameter is 14 cm, is (JEEMAIN Online 13) Al/10 100 (D) 10 uniformly at the rate 8cm ls, then the rate of (B) 10 V10Example 8 Solve xdy ydx = 0 Answer xdy ydx ⇒ xdy =− ydx ⇒ dy y =− dx x = ∫ dy y =− ∫ dx x ⇒ ln e y =− ln e x C ⇒ ln e x ln e y = C ⇒ ln e xy = C ⇒ xy = e C = C 1, say Exercises 2 Solve the differential equation i) x 2 dy dx = y 1 ii) (x 1) y dy dx = y 2Section 1 Theory 3 1 Theory If one can rearrange an ordinary differential equation into the following standard form dy dx = f(x)g(y), then the solution




Y 2xy E X Dx E Xdy 0 Novocom Top




Solve Each Differential Equation Dy Dx 5y E 3x Chegg Com
Solve (y x2y) dy dx =1 Solution y(1x2) dy dx =1!In Introduction to Derivatives (please read it first!) we looked at how to do a derivative using differences and limits Here we look at doing the same thing but using the "dy/dx" notation (also called Leibniz's notation) instead of limits We start by calling the function "y" y = f(x) 1 Add Δx When x increases by Δx, then y increases by ΔySolve the given differential equations 1 dy/dx = x^2/y(1x^3) 2 dy/dxy^2sinx = 0 3 dy/dx = xe^x/ye^y For question (4) dy/dx = 2x/(12y), y(2) = 0 (a) Find the solution of the given initial value problem in explicit form (b) Plot the graph of the solution (c) Determine (at least approximately) the interval in which the solution is defined



Qph Fs Quoracdn Net Main Qimg 4bf



Solve The Differential Equation Dy Dx 1 E X Y Sarthaks Econnect Largest Online Education Community
Experts are waiting 24/7 to provide stepbystep solutions in as fast as 30 minutes!* Solve the following differential equation 3e^x tan y dx (2 e^x) sec^2 y dy = 0 asked Mar 12 in Differential Equations by Takshii (346k points) differential equations;Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more




Solve 2 4 With Details Explanation And Steps Please Chegg Com




Q 3 Find The Integrating Factor And Solve The Exact Solution Consider The Differential Equation E X Y Cosy Cosx 2e 2x Y Dx Sinx E X Y Siny 3y 2e Y Dy Q 5 Prove Socratic
Set the factor '(2xy x 2 1y 2)' equal to zero and attempt to solve Simplifying 2xy x 2 1y 2 = 0 Solving 2xy x 2 1y 2 = 0 Move all terms containing d to the left, all other terms to the rightFree separable differential equations calculator solve separable differential equations stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie PolicyThat passes through the given point Students should have used the method of separation of variables to solve the differential equation Sample 6A Score 9 The student earned all 9 points Sample 6B Score 6 The student earned 6 points 1 point in part (a) and 5 points in part (b) In part (a) the student correctly computes




Ex 9 4 23 General Solution Of Dy Dx E X Y Is A E X E Y C



Secure Media Collegeboard Org Digitalservices Pdf Ap Ap16 Calculus Ab Q4 Pdf
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more Ex 96, 10 For each of the differential equation given in Exercises 1 to 12, find the general solution (𝑥𝑦) 𝑑𝑦/𝑑𝑥=1 Step 1 Put in form 𝑑𝑦/𝑑𝑥 Py = Q or 𝑑𝑥/𝑑𝑦 P1x = Q1 (x y) 𝑑𝑦/𝑑𝑥 = 1 Dividing by (x y), 𝑑𝑦/𝑑𝑥 = 1/((𝑥 𝑦)) 𝑑𝑥/𝑑𝑦 = (𝑥𝑦) 𝑑𝑥/𝑑𝑦 − x = 𝑦 𝑑𝑥/𝑑𝑦 (−1) x murshid_islam said If the boundary condition was , both and would be correct solutions, right?



Secure Media Collegeboard Org Digitalservices Pdf Ap Ap16 Calculus Ab Q4 Pdf




Find The Particular Solution Of The Differential Chegg Com
This is already in the required form (since the xterms are together with dx terms, and yterms are together with dy terms), so we simply integrate `inty^2dyintx^3dx=0` Giving `y^3/3x^4/4=K` This is the general solution for the differential equation We can continue on to solve this as an explicit function in x, as follows `y^3=3(Kx^4/4)`Y(0 )= 5 dy/y = (3 x) dxQuestion Solve The Initial Value Problems Dy/dx = X(y 2)/x^2 4 Y(1) = 5 Dy/dx = Y/x Y(2) = 3 Dy/dx = Y 1/x 1 Y(0) = 0 Dy/dx = Xy Y(1) = 2 Dy/dx = 2y 1 Y(0) = 1/2 Dy/dx = 1/2y 1 Y(0) = 1 Dy/dx = E^y Y = 0 When X = 1 Dy/dx = X/squareroot X^2 9 Y = 5 When X = 4 This problem has been solved!




Find The Solutions To Dy Dx E X Y For Which Y 0 Chegg Com




E Y Dx X 2 2 E Y Dy 0
Dy dx = x2 y = x2 {z} g(x) 1 y {z} f(y) 2 Separate the variables y dy = x2 dx 3 Integrate both sides Z y dy = Z x2 dx y2 2 = x3 3 C 0 4 Solve for y y2 2 = x3 3 C 0 y2 = 2x3 3 C y = r 2x3 3 C Note that we get two possible solutions from the If we didn't have an initial condition, then we would leave the 2in the nal answer, orSolve dy/dx=2xy/(x^2y^2) check_circle Expert Answer Want to see the stepbystep answer? `x e^y = x y` Find `(dy/dx)` by implicit differentiation 2 Educator answers Math Latest answer posted at PM




Ex 9 5 10 Show Homogeneous 1 Ex Y Dx E X Y 1 X Y




Solve The Differential Equation X 2y Dx 2x Y Dy 0 Youtube
There's a much easier way to solve it than Frobenius $\endgroup$ – B Goddard Nov 25 '16 at 15 add a comment 2 Answers 2Taking anti{derivatives of both sides gives 1 2 y2 = 1 3 x3 C There are a number of ways to write this For example 3y2 2x3 = C Observe that for the ODEDy dx = x2 Recall that yis a function of xand so the LHS looks like d dx F(y) by the chain rule The function F(y) = R ydy= 1 2 y2 and so the equation is the same as d dx (1 2 y2) = x2;
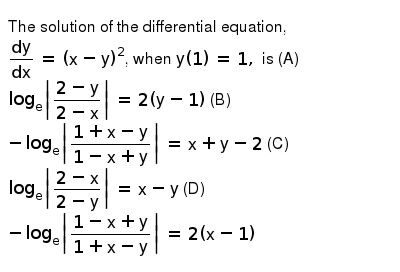



The Solution Of The Differential Equation Dy Dx X Y 2 Whe



Q Tbn And9gcq9arl5ab K Kkztqdma6czzlslnfprp6ljv7o6a18 5qqda4yy Usqp Cau
Example 1 Solve 3y^2e^x dy/dx x^2 = 0 Continuing to use d s o l v e to solve in Python In 7 x=symbols('x') y=Function('y') deq=3*y(x)**2*exp(x)*diff(y(x),x)x**2 ysoln=dsolve(deq,y(x)) #print(ysoln) # Ran this line first Saw that only the third solution is a real functionIf the given curve satisfies the differential equation e y d x (x e y 2 y) d y = 0 and also passes through (0, 0) the possible equation of curve can be Medium View solution Solve the following differential equation x 2 d y (x y y 2) d x = 0, when x = 1 and y = 1 Solve the differential equation e y xDx x2 1 y2 2 = arctanxC ie the solution is y = ± √ 2arctanx2C 53 First order linear ODEs Aside Exact types An exact type is where the LHS of the differential equation is the exact derivative of the product Example 512 x dy dx y = ex ⇒ d dx (xy)=ex ⇒ xy = ex C




The Solution Of Differential Equation Dy Dx E X Y X 2



What Is The Solution Of The Differential Equation Dy Dx 1 E X Y Quora
To solve a separable differential equation Get all the y's on the left hand side of the equation and all of the x's on the right hand side Integrate both sides Plug in the given values to find the constant of integration Solve for y;DEFINITION A differential equation is separable if it is of the form y'=f (x,y) in which f (x,y) splits into a product of two factors, one depending on x alone and the other depending of y alone Thus each separable equation can be expressed in the form y'=Q (x)R (y), where Q and R are given functions When R (y)0 we can divide by R (y) andFree separable differential equations calculator solve separable differential equations stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy




Solve The Following Differential Equations Chegg Com




Engineering Mathematics Notes
X 2 c y 1 x 2 c 1 x 2 Problem 7 Solvedy dx x y cos x 1 sin x Sol Given that dy from MATHEMATICS DIFFERENTI at Gayatri Vidya Parishad College for Degree & PG CoursesSee Answer Check out a sample Q&A here Want to see this answer and more?Differentiate using the Power Rule which states that d d x x n d d x x n is n x n − 1 n x n 1 where n = 2 n = 2 Multiply 2 2 by − 1 1 Reform the equation by setting the left side equal to the right side Reorder factors in −2e−x2 x 2 e x 2 x Replace y' y ′ with dy dx d y d x




Solucionarioecuacionesdiferencialesdenniszill7aedicion P




Solution Of The Differential Equation Dy Dx Y 3 E 2x Y 2 Is Youtube
The differential equation is not well defined in (x,y) = (1,1) as you have an expression of the form 0/0 for dy/dx #8 murshid_islam Example 9 Find the general solution of the differential equation 𝑑𝑦/𝑑𝑥= (𝑥1)/ (2−𝑦) , (𝑦≠2) 𝑑𝑦/𝑑𝑥= (𝑥 1)/ (2 − 𝑦) , (𝑦≠2) (2 − y) dy = (x 1) dx Integrating both sides ∫1 〖 (2−𝑦)𝑑𝑦=〗 ∫1 (𝑥1)𝑑𝑥 2y − 𝑦^2/2 = 𝑥^2/2 x c 〖4𝑦 − 𝑦〗^2/2 = (𝑥Solve The Differential Equation Dy Dx 2y X 2x Y Youtube For more information and source, see on this link https//myoutubecom/watch?v=xzjpbThzkS0




Find The General Solution Of The Differential Equation Dy Dx 1x E Y X Brainly In




Example 17 Show 2y E X Y Dx Y 2x Ex Y Dy 0 Particular
If you mean x * e^(y x^2) then it is quite easy to solve, like so Multiply both sides by (e^(y))dx to get (e^(y)) * dy = (x * dx) * e^(x^2) The antiderivative of the LHS is e^(y) For the RHS, let x^2 = u so that x * dx = du/2 Then the RHS becomes (e^(u)) * du/2 and its antiderivative is (e^(u)) /2 = e^(x^2) / 2 So theWelcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queriesThis is the Solution of Question From RD SHARMA book of CLASS 12 CHAPTER DIFFERENTIAL EQUATIONS This Question is also available in R S AGGARWAL book of CLASS
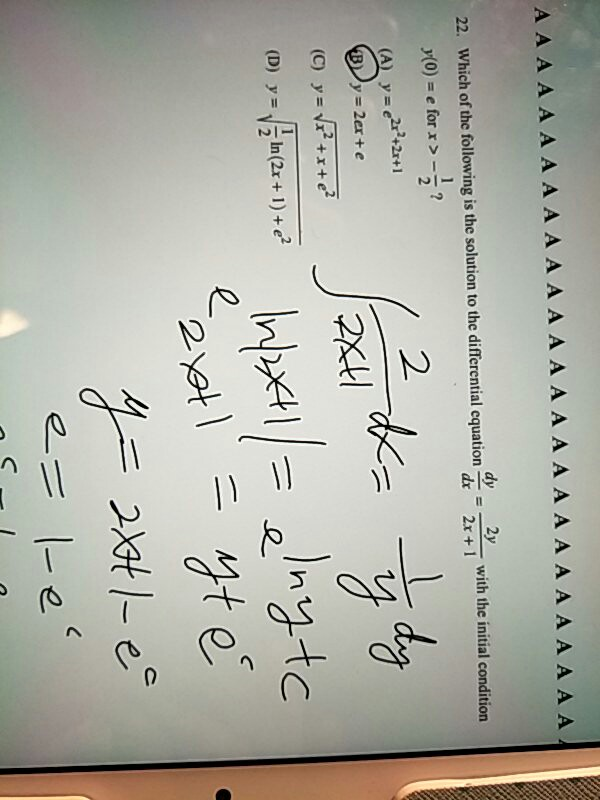



Which Of The Following Is The Solution To The Chegg Com



Q Tbn And9gcrlw5wx6qxsllz2r9p3fgzffnje5hqap6knkskthxk8e15jx7e4 Usqp Cau
To solve, first get into a standard form, multiplying by ex, and integrate (integration by parts for the right hand side) Z ydy = − Z xex dx ⇒ 1 2 y2 = −xe xe C We could solve for the constant before isolating y 1 2 = 01C C = − 1 2 Now solve for y y2 = 2ex(x−1)− 1 2 and take the positive root, since y(0) = 1 y = q 2ex(1−Solve 2xy dy / dx = x 2 y 2, given that y = 0 at x = 1 Solution Express equation in standard form dy / dx = x 2 y 2 / 2 xy , ie quotient of homogenous functions that have same degreeHere we will look at solving a special class of Differential Equations called First Order Linear Differential Equations First Order They are "First Order" when there is only dy dx, not d 2 y dx 2 or d 3 y dx 3 etc Linear A first order differential equation is linear when it can be made to look like this dy dx P(x)y = Q(x) Where P(x) and Q(x) are functions of x To solve it there is a




Ex 9 5 10 Show Homogeneous 1 Ex Y Dx E X Y 1 X Y




Find The Particular Solution Of The Differential Equation Dydx X 3 E 2y Satisfying The Initial Brainly Com
The solution of the differential equation dy/dx = exy x2 ey is (A) y = exy x2 ey c (B) ey ex = x3/3 c (D) ex ey = x3/3 c Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queries




Find Particular Solution Of Y E Y Dx Show That X Y Dy X 2y




For The Differential Equations Find The General Solution Ex Tan Y Dx 1 Ex Sec2 Y Dy 0 Mathematics Shaalaa Com




Differential Equations Separation Of Variables Ppt Download




Differential Equations Separation Of Variables Ppt Download




Differential Equations Ppt Download




Differential Equations Separation Of Variables Ppt Download




1 E Xy Xe Xy Dx Xe X 2 Dy 0 Exact Differential Equation Shorter Solution Youtube




First Order Differential Equations Chapter 2 Ch2 2 Contents 2 1 Solution Curves Without A Solution 2 1 Solution Curves Without A Solution 2 2 Separable Ppt Download



1
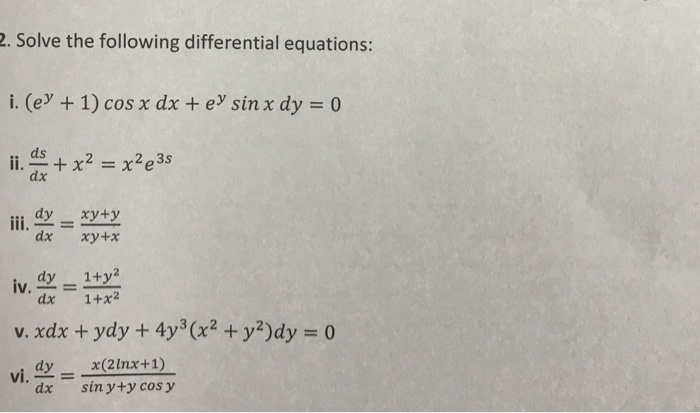



2 Solve The Following Differential Equations I Ey Chegg Com




Solve 2xy 3 Cos X Dx 3x 2 Y 2 Sin Y Dy 0 Chegg Com




Dy Dx E Y Differential Equation Mathematics Stack Exchange
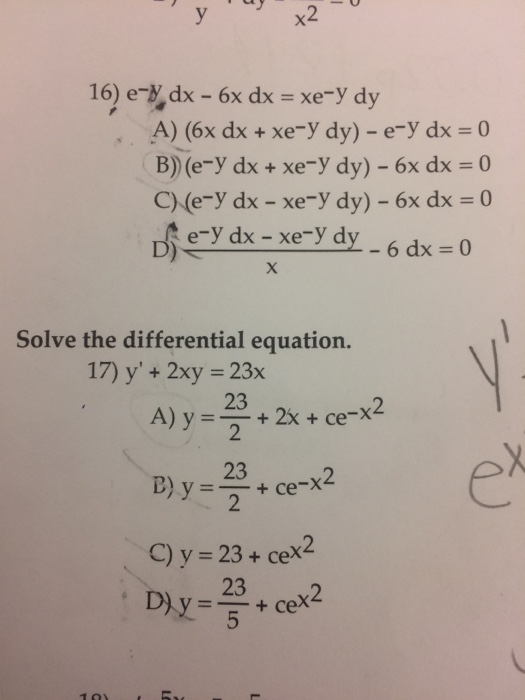



E Y Dx 6x Dx Xe Y Dy 6x Dx Xe Y Dy E Y Chegg Com




Differential Equations Solved Examples Solve The System Of Differential Equations By Systematic Elimination Dx Dt 2x Y Dy Dt 4y




Y 2xy E X Dx E Xdy 0 Novocom Top




If The Solution Of The Differential Equation X Dy Dx Y X E X B E X Y E X Phiv X C Th Youtube




First Order Differential Equations Chapter 2 Ch2 2 Contents 2 1 Solution Curves Without A Solution 2 1 Solution Curves Without A Solution 2 2 Separable Ppt Download



Solve Dx X Dy E Y Sec 2 Y Dy Sarthaks Econnect Largest Online Education Community



If Ex Ey Ex Y Then Dy Dx Quora
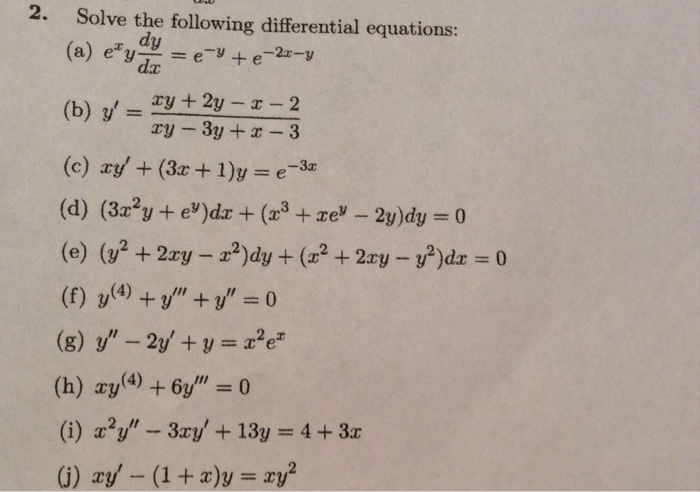



Solve The Following Differential Equation E Xy Dy Dx Chegg Com



Solve The Differential Equation Dy Dx E X Y X 2e Y Sarthaks Econnect Largest Online Education Community



Www Tau Ac Il Levant Ode Solution 6 Pdf
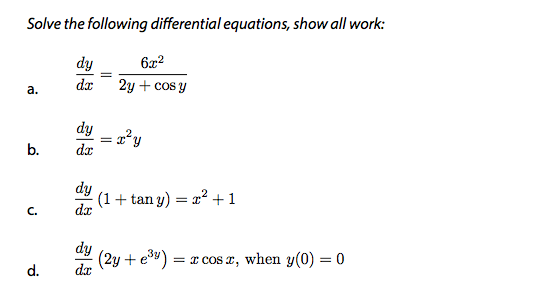



Solve The Following Differential Equations Show All Chegg Com



Dy Dx Xe Y X How Can I Solve The Above Differential Equation Quora




Solve Each Differential Equation Dy Dx X 2y 2 Chegg Com




For Problems 26 Determine An Integrating Factor Chegg Com




Differential Equations Solved Examples Solve The Exact Differential Equation E Y X 2 Sin Y Dx X E Y Cos Y Dy 0




Find The General Solution Of The Following Chegg Com




The Solution Of Dy Dx X 2 Y 2 2x 2 Is




Solve The Differential Equation Dy Dx E X Y X 2e Y
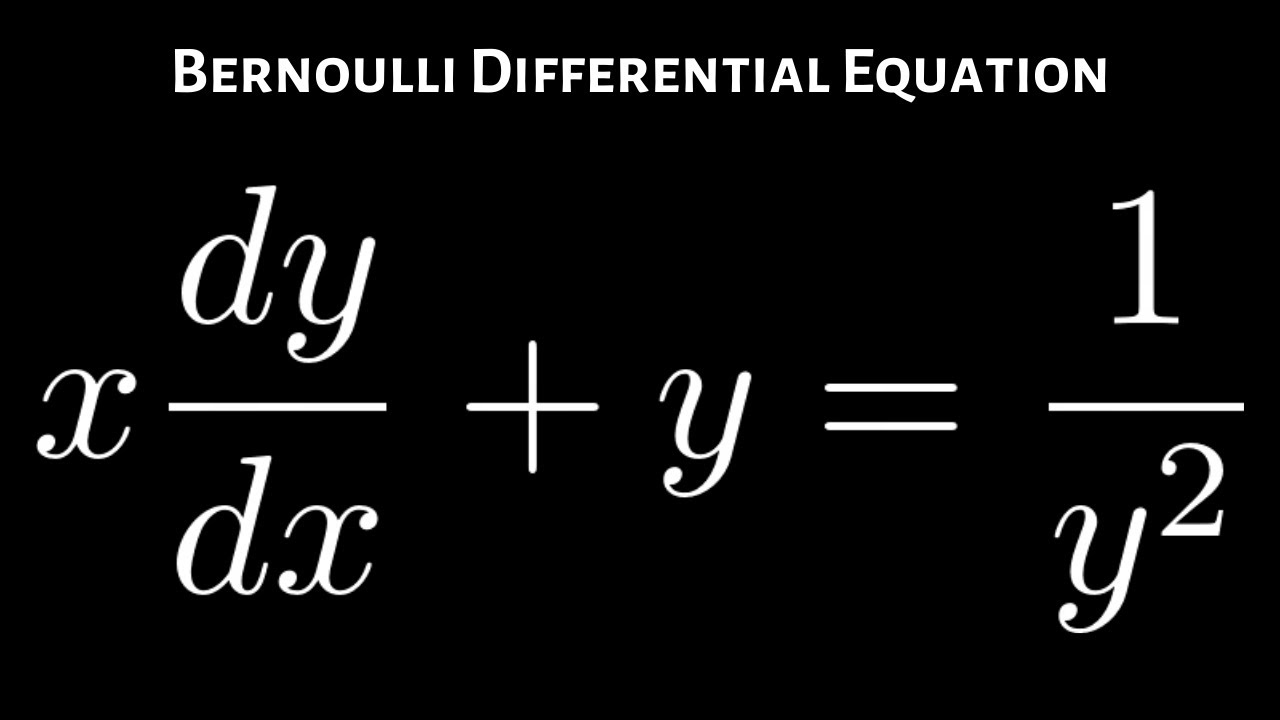



Bernoulli Differential Equation X Dy Dx Y 1 Y 2 Youtube
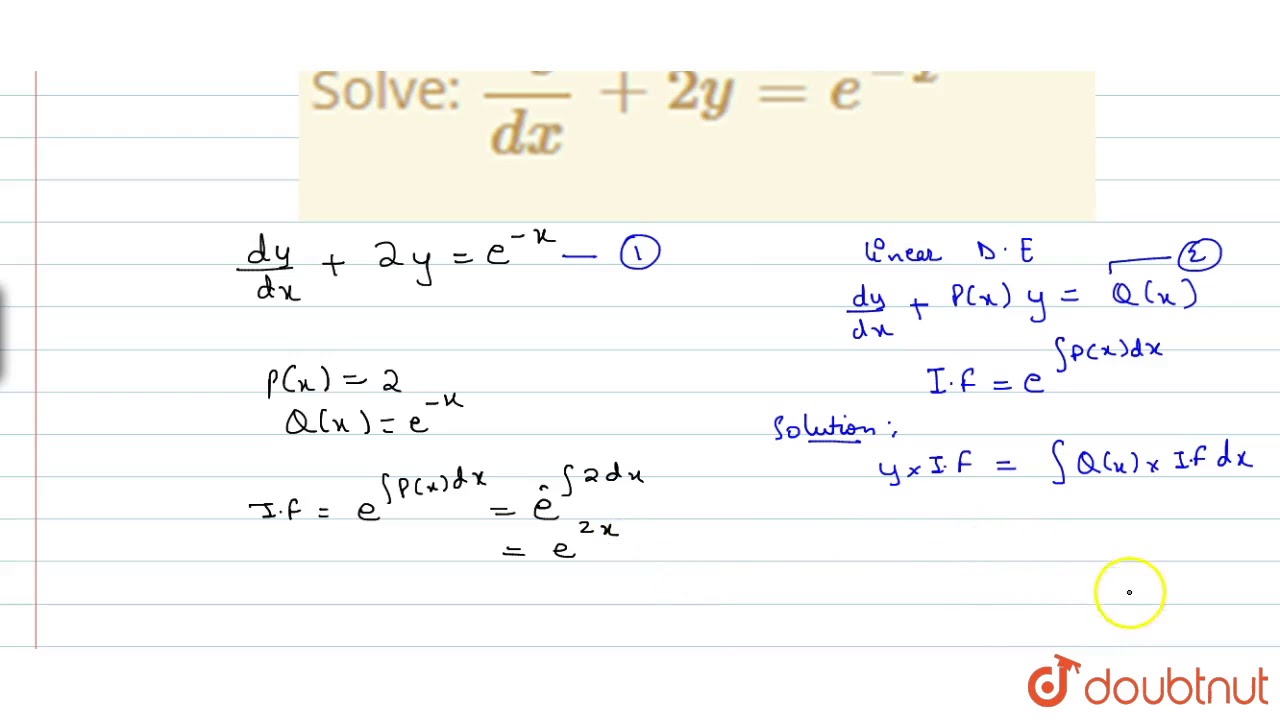



Solve Dy Dx 2y E X Youtube
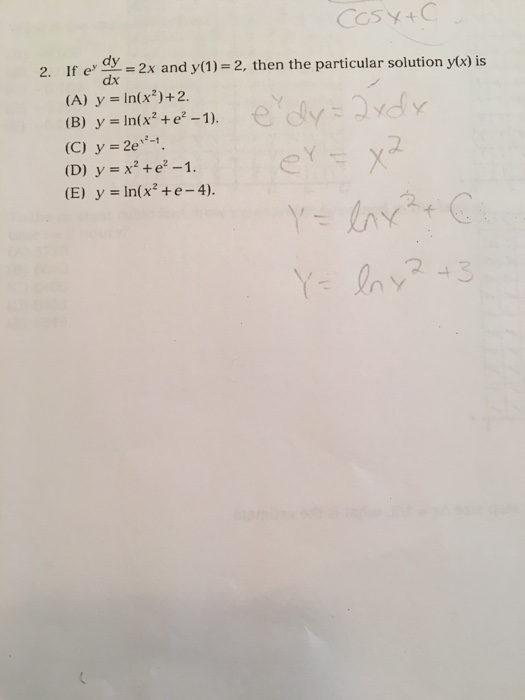



If E Y Dy Dx 2x And Y 1 2 Then The Particular Chegg Com




Ex 9 6 10 Find General Solution X Y Dy Dx 1 Ex 9 6




Solve Each Differential Equation 4 Sec X Dy Csc Y Chegg Com



How To Solve The Separable Differential Equation Dy Dx X 2 E 3y Quora



How To Solve This Exact Equation 2xe Y E X Dx X 2 1 E Y Dy 0 Quora



The Solution Of The Differential Equation Dy Dx E X Y X 2 E Y Is Sarthaks Econnect Largest Online Education Community




Exact Equations Example 3 Video Khan Academy



The Solution Of The Differential Equation Dy Dx E X Y X 2e Y Is Youtube




Solve The Exact Initial Value Problem 2xy Cos Y Chegg Com




The Solution Of The Differential Equation Dy Dx E X Y X 2e Y



Initial Value Problem Dy Dx Y 1 X 3 With Y 1 0 Separable Differential Equation Youtube



Solved Lety F X Y F X Be The Particular Solution To The Differential Equationdy Dx E X 1 E Y Dydx Ex1eywith The Initial Conditionf 1 0 F 1 0 W Course Hero



What Is The Solution Of The Differential Equation Dy Dx 1 E X Y Quora




E Y Dy Dx X 3cosx 2 0




Misc 14 Find Particular Solution X 1 Dy Dx 2e Y 1



Solve The Initial Value Problem Dy Dx 2xy Y 0 Chegg Com




Ex 9 4 10 Find General Solution Ex Tan Y Dx 1 Ex




Differential Equatio Long Answer Questions 7 M R Solye 2x Y 3 Dx 2y X 1 Dy Sol Dy 2x Y 3 Given Equation Is




Misc 18 General Solution Ex Dy Y Ex 2x Dx 0 Miscellaneous




Xy Dy Dx Y 3e X 2 Youtube




Worked Example Identifying Separable Equations Video Khan Academy



What Is The Solution Of The Differential Equation Dy Dx 1 E X Y Quora




Solution Of The Differential Equation 1 E X Y Dx E X Y 1 X




How To Solve Show The Differential Equations Are Exact 2xy Y Tany Dx X 2 X Tany 2 Secy 2 2 Dy 0 Te Tx 2x Dx Dt Xe Xt 0 Quora




The Solution Of The Differential Equation Dy Dx 1 E X Y I




Solve The Separable Differential Equation Dy Dx Chegg Com
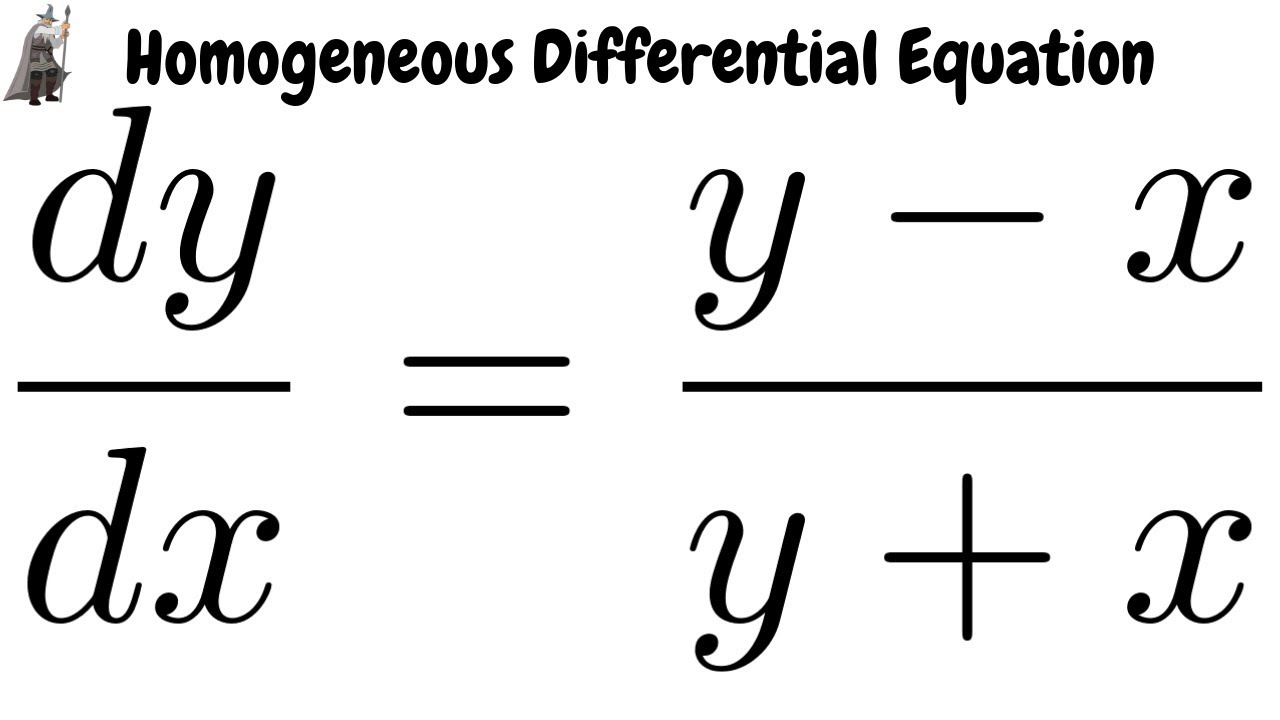



Solving The Homogeneous Differential Equation Dy Dx Y X Y X Youtube




Solucionarioecuacionesdiferencialesdenniszill7aedicion P



How To Solve 1 X 3 Dy Dx X 2 Y Quora




Answered X X 0 Y X X Is A Solution Of Bartleby



Dy Dx Xe Y X How Can I Solve The Above Differential Equation Quora



How To Solve Math E X Y Ye Y Dx Xe Y 1 Dy 0 Math Quora




A Solve The Following First Order Differential Chegg Com




For The Differential Equation X 2 Y 2 Dx 2xy Dy 0 Which Of The Following Are True Youtube




Solve The Given Differentia By Separation Of Chegg Com



Derivative Rules




In Problems 1 26 Solve The Given Differential Chegg Com



Secure Media Collegeboard Org Digitalservices Pdf Ap Ap16 Calculus Ab Q4 Pdf




Differential Equations




Solve The Given Differential Equation By Using An Chegg Com




Misc 14 Find Particular Solution X 1 Dy Dx 2e Y 1




Dy Dx E X Y X2ey Maths Differential Equations Meritnation Com



0 件のコメント:
コメントを投稿